Qiskit : Hello world

qiskit SDK 설치

pip install qiskit

 

런타임 설치

양자 계산을 클라우드 기반에서 실행시키기 위한 런타임입니다. IBM 양자 디바이스에서 실행해야 하기 때문에 오픈소스가 아닙니다.

pip install qiskit-ibm-runtime
pip install qiskit-aer

 

예제 코드에서 사용할 matplotlib을 설치합니다.

pip install matplotlib pylatexenc

 

아래 부터는 window 환경에서 vscode에 wsl로 접속한 후 주피터노트북으로 실행한 코드입니다.

 

ibm에서 제공해주는 동영상에 나오는 예제인데 chatgp에게 해설을 부탁해서 주석으로 추가했습니다.

 

주석 내용중 양자컴퓨팅 프로그래밍에 대한 이해가 필요한 부분은 추후 좀 더 학습한 후 정리해 보겠습니다.

from qiskit import QuantumCircuit

qc = QuantumCircuit(2)  # 2개의 큐비트를 가지는 새로운 양자 회로 객체 qc를 생성

# Hadamard 게이트(H 게이트): 단일 큐비트 게이트 중 하나로, 큐비트를 균등 초양자 상태로 만듬.
# 여기서는 0번 큐비트에만 H 게이트를 적용하므로, 첫 번째 큐비트(0번)은 |0>와 |1>의 중첩 상태가 됨.
qc.h(0) 

# cs(control, target): Controlled-S 게이트를 의미합니다.
# S 게이트는 (1 0   행렬을 가지는 게이트입니다.
#             0 i)
# Controlled-S 게이트는 “제어(control) 큐비트가 |1> 상태일 때만, 타깃 큐비트에 S 게이트를 적용”합니다.
# 이 코드에서는 0번 큐비트가 제어, 1번 큐비트가 타깃이 되어, 0번 큐비트가 |1>일 때만 1번 큐비트에 S 게이트가 적용됩니다.
qc.cs(0, 1)

# qc.draw() 함수는 현재까지 적용된 게이트들을 시각적으로 확인할 수 있는 방법을 제공합니다.
# output='mpl' 옵션은 matplotlib를 사용하여 그래프(이미지) 형태로 그려주며, 주피터 노트북 환경에서는 실행 결과가 바로 노트북 셀에 표시됩니다.
qc.draw(output='mpl')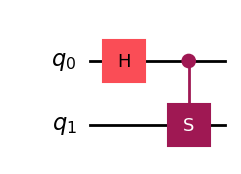

 

 

from qiskit.quantum_info import Pauli
#Pauli 클래스: 문자열(예: "X", "Y", "Z", "I")을 통해 파울리 연산자를 쉽게 만들 수 있습니다. 특히 "XYZI" 등의 문자를 조합하여 여러 큐비트의 텐서곱 형태를 표현할 수 있습니다.


ZZ = Pauli('ZZ')
ZI = Pauli('ZI')
IZ = Pauli('IZ')
XX = Pauli('XX')
XI = Pauli('XI')
IX = Pauli('IX')
# 위에서 Pauli('...')의 인자는 각 큐비트에 어떤 파울리 연산자를 적용할지 나타내는 문자열입니다. 문자열 길이가 2이므로, 2큐비트 연산자입니다.
#
# "Z": 파울리 Z 게이트
# "X": 파울리 X 게이트
# "I": 항등 연산(Identity)
# 예를 들어, ZZ는 두 큐비트에 모두 Z를 적용한 𝑍⊗𝑍 연산자를 의미합니다.
#
# ZZ: 첫 번째 큐비트에 Z, 두 번째 큐비트에도 Z
# ZI: 첫 번째 큐비트에 Z, 두 번째 큐비트에 I(항등)
# IZ: 첫 번째 큐비트에 I, 두 번째 큐비트에 Z
# XX: 첫 번째 큐비트에 X, 두 번째 큐비트에 X
# XI: 첫 번째 큐비트에 X, 두 번째 큐비트에 I
# IX: 첫 번째 큐비트에 I, 두 번째 큐비트에 X
# 이렇게 생성된 ZZ, ZI, IZ, XX, XI, IX는 각각 4×4 행렬로 표현되는 2큐비트 파울리 연산자들입니다.

observables = [ZZ, ZI, IZ, XX, XI, IX]
# 여러 가지 파울리 연산자를 하나의 리스트로 모아둔 것입니다.
# 양자 회로(또는 양자 상태)에 대해 다양한 파울리 연산자의 기댓값(expectation value) 혹은 **측정(measurement)**을 구해야 할 때 유용합니다.
# 예를 들어, 특정 2큐비트 상태 𝜌ρ에 대해 “Z⊗Z” 연산자의 기댓값, “Z⊗I” 연산자의 기댓값 등을 한꺼번에 계산하거나, 동시에 기록하는 상황에서 쓰이곤 합니다.

# 정리
# Pauli 클래스를 이용해 문자열 "Z", "X", "I" 등을 큐비트 개수만큼 이어 붙이면, 그 텐서곱 형태의 파울리 연산자를 빠르게 생성할 수 있습니다.
# "ZZ"는 Z⊗Z, "ZI"는 Z⊗I와 같이 2큐비트 시스템 전체에 적용되는 연산자를 표현합니다.
# 코드에서는 2큐비트에서 자주 쓰이는 여러 조합(ZZ, ZI, IZ, XX, XI, IX)을 만들고, 이를 observables라는 리스트에 모아놓았습니다. 이 리스트는 이후에 양자 상태에 대한 측정, 시뮬레이션, 또는 해밀토니안(Hamiltonian) 구성 등의 용도로 활용될 수 있습니다.
# 이와 같이 from qiskit.quantum_info import Pauli와 문자열을 조합해 여러 파울리 연산자를 편리하게 정의하고, 리스트로 관리해두면 양자 계산 과정에서 다양한 실험(측정, 분석)을 진행할 때 유용합니다.

 

from qiskit_aer.primitives import Estimator 
# Estimator는 양자 회로와 **측정하고자 하는 연산자(Observable)**가 주어졌을 때, 해당 연산자에 대한 기댓값을 효율적으로 계산할 수 있는 도구입니다.

estimator = Estimator() 
# Estimator 객체를 생성합니다. 내부적으로 시뮬레이터(기본적으로 Aer 시뮬레이터)를 사용해 회로를 실행하여 기댓값을 계산하게 됩니다.

job = estimator.run([qc] * len(observables), observables)
#estimator.run(circuits, observables) 형태로 호출되며, Estimator가 계산해야 할 (회로, 관측 연산자) 쌍의 리스트를 받습니다.
#
#첫 번째 인자: [qc] * len(observables)
#  len(observables)의 길이만큼 qc를 복제한 리스트입니다.
#  예를 들어, observables가 6개의 연산자를 담고 있다면, 회로 qc도 6번 반복해서 전달합니다.
#  결과적으로 Estimator는 (qc, ZZ), (qc, ZI), (qc, IZ), (qc, XX), (qc, XI), (qc, IX)처럼 총 6개의 (회로, 관측연산자) 쌍을 받게 됩니다.
#두 번째 인자: observables
#  기댓값을 계산하고 싶은 여러 파울리 연산자(또는 일반 연산자)를 담은 리스트입니다.

#run 메서드: Estimator에게 “이 회로들에 대해 이 연산자들의 기댓값을 구해달라.”고 비동기 요청(Job)을 보내는 역할을 합니다.
#  반환값은 job 객체로, 비동기 실행 결과를 나중에 가져올 수 있는 핸들(handle)입니다.

job.result()
# **job.result()**는 실제로 계산이 완료된 뒤의 기댓값(Expectation Value) 결과를 가져옵니다.
# 반환된 결과(Result 객체) 안에는 주어진 (회로, 관측연산자) 쌍마다 계산된 기댓값이 리스트 형태로 들어 있습니다.
#   예를 들어, observables가 6개라면 6개의 기댓값이 
# [value1, value2, value3, value4, value5, value6] 형태로 들어있을 수 있습니다.
#   만약 측정 시뮬레이션 과정에서 추가 메타데이터(예: 샘플 횟수, 회로 실행 시간 등)가 있으면 함께 포함됩니다.

 

import matplotlib.pyplot as plt
# matplotlib.pyplot: 파이썬에서 가장 널리 쓰이는 2D 그래프 시각화 라이브러리 Matplotlib의 서브 모듈입니다.
# plt 별칭을 통해 그래프를 그릴 수 있는 다양한 함수를 호출합니다.

data = ['ZZ', 'ZI', 'IZ', 'XX', 'XI', "IX"]
values = job.result().values
# data: 문자열 리스트로, 우리가 계산한 관측 연산자들의 이름을 나열합니다. (예: 'ZZ', 'ZI', 'IZ', 'XX', 'XI', 'IX')
# values: job.result().values로부터 가져온 **기댓값(expectation value)**들의 리스트(혹은 NumPy 배열)입니다.
#  예를 들어, 우리가 6개의 관측연산자를 측정했다면, values 내부에는 6개의 숫자가 들어 있을 것입니다.
#  각 값은 (해당 연산자에서 계산된) 기댓값을 의미합니다.

plt.plot(data, values, '-o')
plt.xlabel('Observables')
plt.ylabel('Expectation value')
plt.show()
# 완성된 그래프를 화면에 실제로 표시합니다. 주피터 노트북이나 IPython에서는 자동으로 출력되지만, 일반적인 Python 스크립트 환경에서는 반드시 plt.show()를 호출해 줘야 그래프 창이 나타납니다.

 

참고

https://github.com/Qiskit

https://github.com/Qiskit-Extensions/

https://docs.quantum.ibm.com/guides

https://docs.quantum.ibm.com/guides/install-qiskit

https://docs.quantum.ibm.com/guides/hello-world